Important RGPV Question
Table of Contents
Toggle
CE-503(A), Structural analysis-II
V Sem, CE
UNIT 1
Q.1 Analyze the continuous beam shown in Fig.(a) below by the moment distribution method. Draw the bending moment diagram and shear force diagram, the beam is of uniform section. (RGPV NOV 2023)
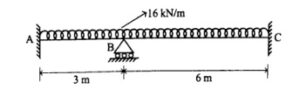
Q.2 Analyse the Rigid frame shown in fig.(1) by Kani’s method. Draw deflected shape and bending moment diagram. (RGPV NOV 2022)
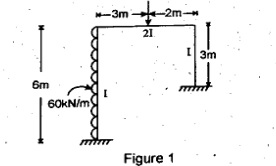
Q.3 Analyse the Rigid frame shown in fig. (2) by moment distribution method. Draw the deflected shape and bending moment diagram. (RGPV NOV 2022)
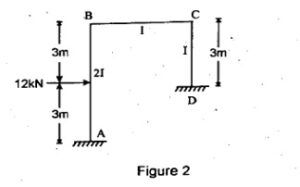
Q.4 Analyses the portal frame shown in Figure, by the moment distribution method. Draw the bending moment diagram. (RGPV DEC 2020)
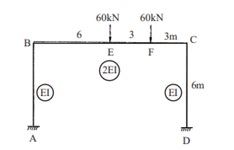
Q.5 Analysis the continuous beam shown in figure by Kani’s method and sketch the B.M diagram that gives all the salient values. (RGPV DEC 2020)
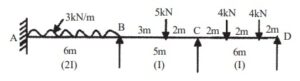
Q.6 Analysis the given frame by the moment distribution method. Draw the bending moment diagram and shear force diagram. (RGPV DEC 2020)
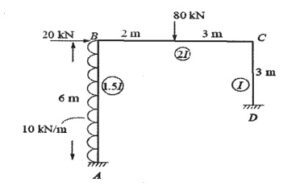
UNIT 2
Q.1 Define the following terms: i) Load Factor ii) Plastic Modulus iii) Plastic neutral axis iv) Relative stiffness v) Distribution Factor vi) Factor of Safety (RGPV NOV 2023)
Q.2 A beam of span 8 m is to be designed for an ultimate u.d.l. of 50 kN/m. The beam is simply supported at the ends. Design a suitable I section using plastic theory, assuming 250 N/mm². (RGPV NOV 2023)
Q.3 Calculate the section modulus, plastic modulus and shape factor for a circular body of radius R. (RGPV NOV 2023)
Q.4 A propped cantilever beam is loaded with uniformly distributed load (UDL) of intensity ‘w’ per unit length over its whole span. If the beam has uniform moment capacity µp, locate the plastic hinges and find the collapse load. (RGPV NOV 2022)
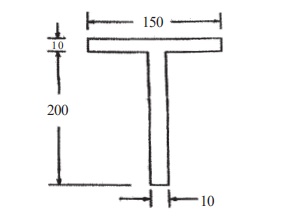
Q.5 Determine the plastic modulus and the shape factor for the T section shown in figure. All dimension in mm. (RGPV DEC 2020)
Q.6 Find the shape factor for circular section. (RGPV DEC 2020)
Q.7 Define the following terms: i) Load Factor ii) Plastic Moment Capacity iii) Working Load iv) Static indeterminacy (RGPV DEC 2020)
UNIT 3
Q.1 Analyze the given frame and draw the bending moment diagram:

(RGPV NOV 2023)
Q.2 Explain how the wind and earthquake loads are accounted for in the analysis of tall building frames? (RGPV NOV 2022)
Q.3 State various codal provisions for lateral loads, as per BIS, for the analysis of tall building frames. (RGPV NOV 2022)
Q.4 Analysis the building frame by portal frame method. Assume point of inflection at 0.1L for gravity load. Draw BMD.
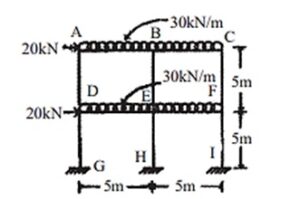
(RGPV DEC 2020)
Q.5 Write a short note on structural behavior of tall buildings subjected lateral forces.
(RGPV DEC 2020)
UNIT 4
Q.1 Analysis the continuous beam shown in figure by flexibility matrix method.
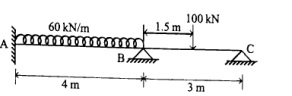
(RGPV NOV 2023)
Q.2 Using Stiffness method analyse the beam shown in fig. (3). El is constant.
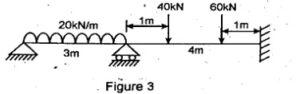
(RGPV NOV 2022)
Q.3 Analyse the continuous beam shown in fig. (4) using flexibility method. (RGPV NOV 2022)
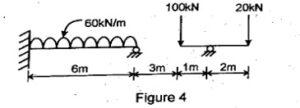
Q.4 Analysis the continuous beam shown in figure by stiffness matrix method. Take EI is constant. (RGPV DEC 2020)
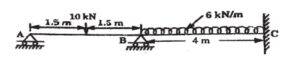
UNIT 5
Q.5 Explain influence line diagram for indeterminate structures and Muller Breslau Principle. (RGPV NOV 2023)
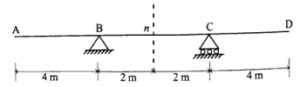
Q.6 For the double overhanging beam shown in Figure (a), construct the influence lines for the support reactions at B and C and the shearing force and the bending moment at section n. (RGPV NOV 2023)
Q.7 Using Muller Breslau principle, compute the influence line ordinates for:
i) Reaction at fixed end ii) Moment at mid span
For the propped cantilever beam of 8m span and having uniform EL. (RGPV NOV 2022)
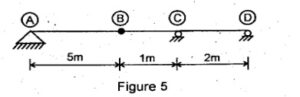
Q.8 For the continuous beam shown in fig. (5) obtain the ordinates of influence line and draw ILD for (RGPV NOV 2022)
i) Reaction at (A) ii) Shear force and bending moment at (B)
Q.9 State and explain Muller-Breslau principle. (RGPV DEC 2020)
Q.10 State the influence line diagram and its advantage. (RGPV DEC 2020)
— Best of Luck for Exam —
