Important RGPV Question

EX-703 (C) Digital Signal Processing

VII Sem, EX

UNIT-I

Q.1 Explain the procedure of representing the sequence of samples with suitable examples. Also define the length of a discrete time signal. (RGPV Nov 2023)

Q.2 Find the product and addition for following two sequences

g[n] = [- 21, 1.5, 3] for  

c[n] = [3.2, 41, 36, – 9.5, 0] for  

Also define Nyquist rate.

(RGPV Nov 2023)

Q.3 Classify the discrete time signal with respect to symmetry exhibited by samples with respect to time index n = 0 with suitable examples. (RGPV Nov 2023)

Q.4 Determine whether the following system are linear, time-invariant and causal: (RGPV DEC 2020)

i) y(n)=x(n) cos x(n)

ii) y(n) = x(-n+2)

iii) y(n) = n x²(n)

UNIT-II

Q.1 Define z-transform and region of convergence of a sequence. Also explain the causal and anti-causal systems. (RGPV Nov 2023)

Q.2 Determine the z-transform of the finite length sequence

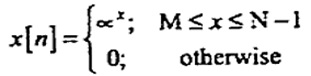
Also determine its ROC.

(RGPV Nov 2023)

Q.3 Explain the properties of z-transform for causal signals. (RGPV Nov 2023)

Q.4 How is stability of a system determined with z-transform? (RGPV Nov 2023)

UNIT-III

Q.1 Discuss the Discrete Fourier transform of length N-time domain sequence x[n]. (RGPV Nov 2023)

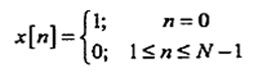
Q.2 Compute the N-point DFT for a sequence over  (RGPV Nov 2023)

Q.3 State and prove following properties of DFT. (RGPV DEC 2020)

i) Circular Frequency Shift

ii) Periodicity

Q.4 Obtain the Fourier transform of: (RGPV DEC 2020)

x(t)=5[u(t+3)=u(t+2)-u(t-2)-u(t-3)]

Q.5 Write the applications of FFT. State its computational requirements. (RGPV DEC 2020)

UNIT-IV

Q.1 Describe the direct form and cascade form of a basic FIR digital filter. (RGPV Nov 2023)

Q.2 An IIR filter transfer function is expressed as

 

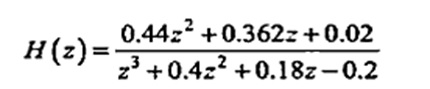
Realize its direct form II with its diagram. (RGPV Nov 2023)

Q.3 Obtain the cascade form realizations of FIR systems

H(z) = 1+5/2 Z^-1+2 Z^-2+2 Z^-3 (RGPV DEC 2020)

Q.4 Convert the analog filter into a digital filter whose system function is 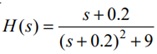 technique. Assume T = 1s. Use impulse invariant (RGPV DEC 2020)

Q.5 Discuss the realization of IIR filters in canonic and parallel forms. (RGPV DEC 2020)

UNIT-V

Q.1 Write down the applications of digital signal processing. Also differentiate the strict sense stationary and wide sense stationary processes. (RGPV Nov 2023)

Q.2 Explain the optimal filtering with suitable examples. (RGPV Nov 2023)

Q.3 Explain the following window techniques for designing FIR filters. (RGPV DEC 2020)

a) Kieser window

b) Hamming window

EXTRA QUESTIONS

Q.1 Discuss the orthogonal transform pair for x[n] of length N with X[k] coefficients of N-point orthogonal transform. (RGPV Nov 2023)

Q.2 Explain how the total number of multipliers can be reduced. Give a suitable example. (RGPV Nov 2023)

Q.3 Write short notes on any one of the following: (RGPV Nov 2023)

i) Window method

ii) Park-McClellan’s method

Q.4 Write short notes on (any two): (RGPV DEC 2020)

i) One sided Z-transform

ii) FIR Digital Filters Characteristics

iii) Bilinear Transformation Method

Q.5 Compute the response of the system: (RGPV DEC 2020)

y(n)=0.7y(n-1)-0.12y(n-2)+x(n-1)+x(n-2)

to the input x(n) = n u(n). Is the system stable.

— Best of Luck for Exam —