Important RGPV Question
Table of Contents
ToggleAL-601 Theory of Computation
VI Sem, AIML
UNIT 1-Introduction Of Automata Theory
Q.1) Design a Moore machine to determine the residue of mod 2 of the input treated as a binary string.
(RGPV Dec 2024)
Q.2) Find an equivalent ϵ-NFA for the following regular expression (0+1)∗011.
(RGPV Dec 2024)
Q.3) Explain “Finite State Machines with Outputs”. Discriminate between Mealy and Moore machines.
(RGPV May 2024)
Q.4) What is Moore Machine? How Moore machine can be converted into Mealy Machine? Explain with the help of an example.
(RGPV May 2023)
Q.5) Explain briefly about the composite machine with an example.
(RGPV May 2023)
UNIT 2-Types Of Finite Automata
Q.1) Convert the Ʌ NFA to NFA.
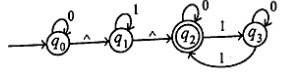
(RGPV Dec 2024)
Q.2) Derive regular expression from this Finite Automata.
(RGPV Dec 2024)

Q.3) Define regular language and regular expressions. Find regular expression for the following: Language of all string that do not end with 01.
(RGPV Dec 2024)
Q.4) Say whether the NFA accepts the following or not
i) abaa
ii) abab
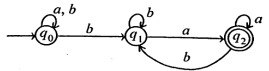
(RGPV May 2024)
Q.5) Construct a NFA second last symbol is zero over the alphabet {0, 1} then convert in DFA.
(RGPV May 2024)
Q.6) Design a DFA which accept the string starting symbol differ from ending symbol over the alphabet {0, 1}. Show dead state if any.
(RGPV May 2024)
Q.7) Minimize the following automata.
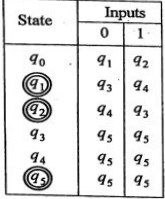
(RGPV May 2024)
Q.8) State pumping lemma for regular languages. Prove that the language {an∣n is prime number} is not regular.
(RGPV May 2024)
Q.9) Describe how Finite automata can be called a language acceptor?
(RGPV May 2023)
Q.10) Find out the Regular Expression from given DFA.
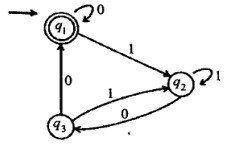
(RGPV May 2023)
Q.11) Obtain the regular expression for the following set:
i) Set of all strings over Σ={a,b} with exactly two a.
ii) L={ax∣x is divisible by 3 or 5}.
(RGPV May 2023)
Q.12) Show that L = {anbncn∣n≥1} is not CFL.
(RGPV May 2023)
UNIT 3-Grammars
Q.1) Convert the grammar {S→ABaC∣ABa, A→Aa|a, B→BaB∣b, C→CC} Chomsky normal form.
(RGPV Dec 2024)
Q.2) Define formally Type 0, Type 1, Type 2 and Type 3 grammar. Show the corresponding automata for each class.
(RGPV Dec 2024)
Q.3) Convert to Greibach normal form. (S→AB∣AA, A→aA∣a, B→Sb∣b).
(RGPV Dec 2024)
Q.4) Derive any two representative strings with minimum length 4 from following context free grammar. G=({S,A,B},{a,b},P,S) S→bA∣aB A→aA∣aS∣a B→bB∣bS∣b.
(RGPV Dec 2024)
Q.5) Construct context free grammar for L = {wcwR | w in (a+b)*}, Reverse of w is denoted as wR.
(RGPV May 2024)
Q.6) Find the Greibach normal form grammar equivalent to the following:
CFG: S→ABA→BS∣B→SA∣0.
(RGPV May 2024)
Q.7) What do you mean by Parsing? How left most and right most derivation helps to find out the ambiguity in a grammar?
(RGPV May 2024)
Q.8) What do you mean by Closure properties of regular languages? Define some important closure properties.
(RGPV May 2023)
Q.9) Differentiate between Context-Free Grammar and Context-Sensitive Grammar.
(RGPV May 2023)
Q.10) Write CFG for regular expression (011)∗(01)∗01∗.
(RGPV May 2023)
UNIT 4-Push Down Automata
Q.1) Construct PDA for the language wcwR where w is string of zeros and ones.
(RGPV Dec 2024)
Q.2) Construct a PDA accepting by empty stack each of the following language:
i) anbmcndm where n,m≥1
ii) anbncm|n≥0
(RGPV Dec 2024)
Q.3) Define a deterministic PDA. How a DPDA differs from a non-deterministic PDA?
(RGPV May 2024)
Q.4) Construct a PDA accepting by empty stack each of the following language.
i) anbmcn where n,m≥1
ii) anb3n∣n≥0
(RGPV May 2024)
Q.5) Design PDA to accept the language L(G) = {anbman∣m,n≥1}.
(RGPV May 2023)
Q.6) Design a PDA which recognizes the set of all even length palindromes over {a, b}.
(RGPV May 2023)
Q.7) What is PDA? Explain instantaneous description of PDA.
(RGPV May 2023)
UNIT 5-Turing Machine
Q.1) Design a Turing Machine that accepts the language 1n0n where n>0.
(RGPV Dec 2024)
Q.2) What is a Turing machine? Give the specification of a Turing machine and explain.
(RGPV Dec 2024)
Q.3) Design a Turing Machine which computes the multiplication of two numbers.
(RGPV May 2024)
Q.4) Design a Turing Machine for the language {L(G) = anbn∣n≥1}.
(RGPV May 2023)
Q.5) Explain P class problems in detail.
(RGPV May 2023)
Extra Questions-
Q.1) Write a short note (any three):
i) Recursively Enumerable
ii) GNF
iii) Derivation Tree
iv) Mealy Machine
(RGPV Dec 2024)
Q.2) Write short note on (any three):
i) Halting problem
ii) Decidability
iii) Mealy Machine
iv) CNF (Chomsky Normal Form)
(RGPV May 2024)
Q.3) Write short note on any two of the following:
i) NP Hard
ii) Petri Net Model
iii) Halting problem of Turing machine
iv) 2-way DFA
(RGPV May 2023)
— Best of Luck for Exam —

