Important RGPV Question
Table of Contents
Toggle
CE-501, Fluid Mechanics-I
V Sem, CE
UNIT 1
Q.1 Describe in brief about the Surface tension and Pressure intensity inside a droplet, a bubble and a liquid jet. (RGPV NOV 2023)
Q.2 If a density of a liquid is 840 kg / m3 and kinematics viscosity is 1.70 St, find its specific weight, specific gravity, specific volume and coefficient of viscosity. (RGPV NOV 2023)
Q.3 Define Pascal law and intensity of pressure. (RGPV NOV 2023)
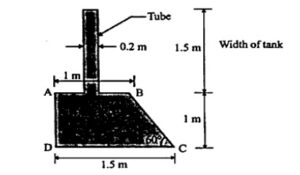
Q.4 Determine the total forces and pressure distribution diagram for the surface AB, BC, CD and DA and also locate the centre of pressure for the surface BC. (RGPV NOV 2023)
Q.5 Explain the following terms in details: 1) Viscosity ii) Compressibility iii) Surface Tension iv) Capillarity (RGPV DEC 2020)
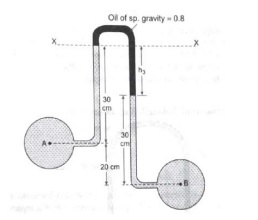
Q.6 An inverted differential manometer is connected to two points A and B which convey water. The fluid in manometer is oil of sp. gravity 0.8. For the manometer readings shown in the figure, find the pressure difference between A and B. (RGPV DEC 2020)
Q.7 What is the relation between gauge pressure, absolute pressure, vacuum pressure and atmospheric pressure. (RGPV DEC 2020)
Q.8 Define a fluid and distinguish between compressible and incompressible fluids. (RGPV DEC 2020)
Q.9 With neat sketches, explain the conditions of equilibrium for floating and sub-merged bodies. (RGPV JUN 2020)
Q.10 Give reasons for the following. i) Viscosity changes with temperature rise. ii) Mercury (Hg) is preferred as a manometric liquid. iii) Free surface of water in a capillary tube is concave. iv) Light weight objects can float on the free surface of liquids. (RGPV JUN 2020)
Q.11 A liquid bubble of 2 cm radius has an internal pressure of 12.95 Pascals. Determine the surface tension of the liquid film. (RGPV JUN 2020)
Q.12 Define the following terms: a) Capillarity b) Surface tension c) Mass density d) Pressure intensity e) Kinematic viscosity (RGPV JUN 2020)
UNIT 2
Q.1 Describe in brief about the Potential function, Stream Function and Flow net. (RGPV NOV 2023)
Q.2 If the velocity component is given by
U = 8 + 4xy + t2 ; V = -(xy + 20t) ; W = 5x + y
Find velocity and acceleration of a particle at (3, 2, 1) t = 1 sec. (RGPV NOV 2023)
Q.3 With the help of a diagram explain Stream lines, equipotential lines and flow net. Prove that equipotential lines and stream lines intersect each other orthogonally. (RGPV DEC 2020)
Q.4 Derive an expression for total pressure and center of pressure on an inclined plane surface submerged in the liquid. (RGPV DEC 2020)
Q.5 Define the following: i) Buoyancy and Center of buoyancy ii) Meta Center and Meta centric Height (RGPV DEC 2020)
Q.6 Explain Potential function. The velocity in a flow field is given by u3 m/s, v = 6 m/s. Determine the equation of the streamline passing through the origin and the one passing through a point (2 m, 3 m). (RGPV JUN 2020)
Q.7 Explain what do you understand by: i) Total Acceleration ii) Local Acceleration iii) Convective Acceleration (RGPV JUN 2020)
Q.8 Show that streamlines and equipotential lines are orthogonal to each other. (RGPV JUN 2020)
UNIT 3
Q.1 Derive an Equation of Bernoulli’s Theorem by using Euler Equation of motion along a streamline. (RGPV NOV 2023)
Q.2 Write the Assumption, Limitation and Modification of the Bernoulli’s Theorem. (RGPV NOV 2023)
Q.3 Explain the difference between Venturi meter and Orifice meter. (RGPV NOV 2023)
Q.4 Derive the Expression for the measurement of Discharge using Orifice Meter. (RGPV NOV 2023)
Q.5 Describe in brief about the Weirs and Notches. (RGPV NOV 2023)
Q.6 What is venturi meter? Write the formula for calculation the flow from venturi meter. (RGPV DEC 2020)
Q.7 Derive Euler’s equation of motion along a stream line and hence derive the Bernoulli’s theorem. (RGPV DEC 2020)
Q.8 Explain the dimensional homogeneity, with an example. (RGPV JUN 2020)
Q.9 The resistance of motion ‘R’ for a sphere of diameter ‘D’ moving at constant velocity ‘v’ through a compressible fluid is dependent upon the density ‘p’ and the bulk modulus “K”. The resistance is primarily due to the compression of the fluid in front of the sphere. Show that the dimensionless relationship between these quantities is Ne function (Ma). (RGPV JUN 2020)
Q.10 Derive the equation linking velocity u and height y at a given point in the x direction when the flow is laminar between two stationary flat parallel plates distance h apart. Go on to derive the volume flow rate and mean velocity. (RGPV JUN 2020)
Q.11 Explain with neat sketch, working of pitot-static tube. (RGPV JUN 2020)
Q.12 Bernoulli’s theorem for the steady flow of an incompressible fluid. Derive an expression for Bernoulli’s equation from the first principles. (RGPV JUN 2020)
UNIT 4
Q.1 Define the following. i) Bulk Modulus ii) Reynolds number iii) Stoke’s Law iv) Stream Lines (RGPV NOV 2023)
Q.2 Derive the expression for the Velocity Distribution and Shear stress distribution for the flow of a viscous fluid between two parallel fixed plate. (RGPV NOV 2023)
Q.3 A 150 mm diameter pipe carries liquid in laminar regime. At a radial distance of 20 mm from the axis of pipe the velocity is 0.4 m/sec calculate: i) Max velocity ii) Mean velocity iii) Discharge of pipe in Ips 150 (RGPV NOV 2023)
Q.4 A rectangular plate which is 2m wide and 3 meter long is immersed vertically in a fluid of relative density 1.6 in such a way that its 2 meter side is kept horizontal. Plate is kept 1.0 meter below the free surface of water. Find the total pressure on the plate. (RGPV DEC 2020)
Q.5 The velocity potential for a two-dimensional flow is, x(2y-1). Determine the velocity at the point P(4,5). Also obtain the value of stream function at this point P. (RGPV DEC 2020)
Q.6 For laminar flow of an oil having dynamic viscosity u1.766 Pa.s in a 0.3m diameter pipe, the velocity distribution is parabolic with a maximum point velocity. of 3 m/s at the center of the pipe. Calculate the shear stresses at the pipe wall and within the fluid 50mm from the pipe wall. (RGPV DEC 2020)
Q.7 The terminal velocity of a steel sphere falling in a liquid is 0.03 m/s. The sphere is 1 mm diameter and the density of the steel is 7830 kg/m³. The density of the liquid is 800 kg/m³. Calculate the dynamic and kinematic viscosity of the liquid. (RGPV JUN 2020)
Q.8 If the velocity distribution of a fluid over plate is given by u = (3/4) y – y 2 , where u is the velocity in meter per second at a distance of y meter above the plate, determine the shear stress at y = 0.15 meter. Take dynamic viscosity of fluids 8.5 x 10-5 kg -sec/m2 (RGPV JUN 2020)
UNIT 5
Q.1 A pump is pumping water at the rate of 7536 lit/min. The pump inlet is 40 cm in diameter and the vacuum pressure over there is 15 cm of Mercury. The pump outlet is 20 cm in diameter and it is 1.2 m above the inlet. The pressure at the Outlet is 107.4 kN/m². Estimate the power added by pump. (RGPV NOV 2023)
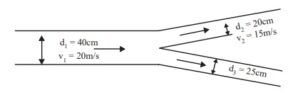
Q.2 A 40 cm diameter pipe, conveying water branches into two pipes of diameters 20 cm and 25 cm respectively. If the average velocity in the 40 cm diameter pipe is 20 m/s, find the discharge in this pipe. Also determine the velocity in 25 cm pipe if the average velocity in 20 cm diameter pipe is 15 m/s. (RGPV DEC 2020)
Q.3 The pressure drop Ap, along a straight pipe of diameter D has been experimentally studied, and it is observed that for laminar flow of a given fluid and pipe, the pressure drop varies directly with the distance I, between pressure taps. Assume that Ap is a function of D, I, the velocity V, and the fluid viscosity u. Use dimensional analysis to deduce how the pressure drop varies with pipe diameter. (RGPV DEC 2020)
Q.4 What should be the diameter of a droplet of water. If the pressure inside is to be 0.0018 kg(f)/cm² greater than the outside? Given the value of surface tension of water in contact with air at 20°C as 0.0075 kg(f)/m. (RGPV JUN 2020)
Q.5 A 100 meters long pipeline connects two reservoirs. The difference in water levels is 15 meters. The pipeline has two equal sections of 50 meters each. Diameters of first and second sections are 25 mm and 50 mm respectively. If the friction coefficient of pipe material is 0.005, determine the velocity of water flow through the two sections and the rate of water flow in liters/sec. Represent TEL and HGL. (RGPV JUN 2020)
— Best of Luck for Exam —

