Important RGPV Question
Table of Contents
Toggle
CE-604(D) Operation Research,
VI Sem, CE
UNIT 1-Linear Models
Q.1 Explain the Phases of Operation Research. (RGPV MAY 2023)
Q.2 Define Model. Discuss the steps of modeling. (RGPV MAY 2023)
Q.3 Explain the characteristics of operation research and state the limitations of O.R. models. (RGPV MAY 2022)
Q.4 Use simplex method to solve the following Linear programming problem: (RGPV MAY 2022)
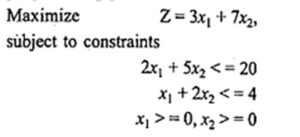
UNIT 2-Transportations Models
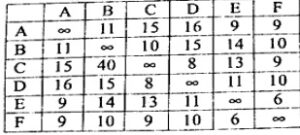
Q.1 Solve the following travelling salesman problem. (RGPV MAY 2023)
Q.2 What is degeneracy in Transportation Problem? Discuss its consequence and how it is overcome? (RGPV MAY 2022)
Q.3 A project being planned involved the following activities: (RGPV MAY 2022)
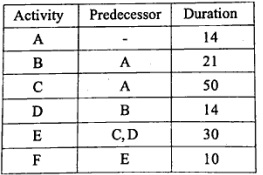
i) Construct the network diagram and find out critical path and project completion time.
ii) Determine expected project completion time.
iii) Determine free slack and total slack
UNIT 3-Inventory Models
Q.1 Explain Economic order quantity model with suitable example. (RGPV MAY 2023)
Q.2 In the basic EOQ model, if D=6000 per year, S= $150, and holding cost – $15 per unit per month, Unit cost=$5, what is the economic order quantity? (RGPV MAY 2023)
Q.3 Briefly explain queuing systems and its characteristics. (RGPV MAY 2022)
Q.4 Postal clerk can service a customer in 3 minutes. The service time is being exponentially distributed. The inter arrival time of customers is also exponentially distributed with an average of 12 minutes during early morning slack period and an average of 5 minutes during the afternoon peak period. Assess the average queue length and the expected waiting time in the queue during the two periods. (RGPV MAY 2022)
UNIT 4-Queueing Models
Q.1 Define Queue. Explain Queuing systems with neat sketch. (RGPV MAY 2023)
Q.2 A television repairman finds that the time spent on his jobs has exponential distribution with a mean of 30 minutes. If he repairs the sets in the order in which they came in, and if the arrival of sets follows a Poisson distribution with an approximate average rate of 10 per 8-hour day, what is repairman expected idle time each day? (RGPV MAY 2023)
 https://forms.gle/SLQ1msNT77dMJrim8
https://forms.gle/SLQ1msNT77dMJrim8
UNIT 5-Decision Models
Q.1 Draw a network diagram and find the critical path of diagram. (RGPV MAY 2023)
![]()
EXTRA QUESTIONS
Q.1 The owner of a chain of four grocery stores has purchased six crates of fresh strawberries. The estimated probability distribution of potential sales of the strawberries before spoilage differs among the four stores. The following table gives the estimated total expected profit at each store, when it is allocated various numbers of crates. (RGPV MAY 2023)
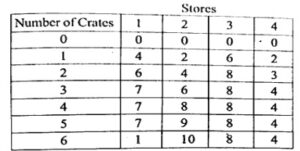
For administrative reasons, the owner does not wish to split crates between stores. However he is willing to distribute zero crates to any of his stores.
Q.2 Write short notes on the following: (RGPV MAY 2023)
a) PERT
b)Pay off matrix
c) Saddle Point
d) Zero Sum Game
Q.3 Write about the following: (RGPV MAY 2023)
- a) Stochastic inventory models
- b) Minimal spanning tree
Q.4 SBC, a company that buys alarm clocks from a manufacturer and distributes to retailers. SBC would like to reduce its inventory cost by determining the optimal number of alarm clocks to obtain per order. The annual demand is 1,000 units, the ordering cost is $10 per order and the carrying cost is $0.50 per unit per year. Each alarm clock has a purchase cost of $5. How many clocks should SBC order each time? (RGPV MAY 2022)
Q.5 A Police Station employs 30 police officers. Each officer works for 5 days per week. The crime rate fluctuates with the day of week, so the number of the police officers required each day depends on which day of the week it is: Monday, 18; Tuesday, 24; Wednesday, 25; Thursday, 16; Friday, 21; Saturday, 28; Sunday, 18. The Police Station wants to schedule police officers to minimize the number whose days off are not consecutive. Formulate an LP that will accomplish this goal. (RGPV MAY 2022)
Q.6 Explain the following terms: (RGPV MAY 2022)
i) Pay off matrix
ii) Fair Game
iii) Rule of dominance
iv) Saddle Point
Q.7 Solve the given problem using Big-M method: (RGPV MAY 2022)

Q.8 Define: (RGPV MAY 2022)
i) Basic Feasible Solution
ii) Optimal Solution
iii) Un-bound solution
Q.9 A project consists of activities as given in the table: (RGPV MAY 2022)
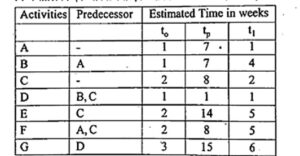
i) Draw the Project network.
ii) Identify the critical path and determine the expected completion time for project.
iii) What is the probability that project would be completed in 17 weeks.
Q.10 Explain in brief the following terms related to ‘Service discipline’ with examples. (RGPV MAY 2022)
i) FIFO ii) LIFO iii) Priority Service iv) Random Service
— Best of Luck for Exam —
