Important RGPV Question

CSIT- 503 (A) Theory of Computation

V Sem, CSIT

UNIT 1-Introduction of the theory of computation

Q.1) Compute the Regular Expression for the DFA as shown below

(RGPV Nov 2022)

Q.2) Design DFA’s for detecting 1100 Sequence with Overlap over the alphabet Sigma = {0, 1}

(RGPV Nov 2022)

Q.3) Convert the following NFA to an equivalent DFA. (RGPV Nov 2022)  

UNIT 2-Regular grammars, regular expressions, regular sets

Q.1) Find a regular grammar that generates the language on (a, b) consisting of all strings with at most one a’s and more than two b’s.

(RGPV Nov 2022)

Q.2) Find a regular grammar that generates the language on {a,b} consisting of all strings with exactly one a’s and no more than two b’s.

UNIT 3- Introduction of Context-Free Grammar

Q.1) Construct context free grammars to accept the language L(G)= { aⁿ b^m c^m d²ⁿ |n>=0,m>0} over the alphabet,  = {a, b, cd} 

(RGPV Nov 2022)

Q.2) Given the following ambiguous context free grammar

S→Ab| aaB

A→a| Aa

B→b

(RGPV Nov 2022)

Q.3) Find the strings generated by the grammar that has two leftmost derivations. Show the derivations.

(RGPV Nov 2022)

Q.4) Show the two derivation trees for the string S.

(RGPV Nov 2022)

Q.5) Find an equivalent unambiguous context-free grammar.

(RGPV Nov 2022)

Q.6) Give the unique leftmost derivation and derivation tree for the string s generated from the unambiguous grammar above.

(RGPV Nov 2022)

UNIT 4- Introduction of PDA, formal definition

Q.1) Construct Non-Deterministic Pushdown Automata (NPDA) to accept the language {w/w starts and ends with the same symbol} over the alphabet. Σ = {0, 1}

(RGPV Nov 2022)

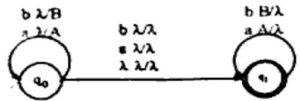
Q.2) Construct corresponding CFG for the following NPDA. (RGPV Nov 2022)

UNIT 5-Turing machines

Q.1) Construct Turing Machine (TM) to accept the language L= {0 ⁽²ⁿ⁾  | 1ⁿ | 2⁽²ⁿ⁾ |n>=0} over the alphabet, Σ = {0, 1, 2}.

(RGPV Nov 2022)

Q.2) Prove that the problem of determining whether for a Turing machine M there is some input string for which M halts is undecidable.

(RGPV Nov 2022)

Q.3) Prove that the recursive languages are closed under union, intersection, and complement.

(RGPV Nov 2022)

— Best of Luck for Exam —