Important RGPV Question
Table of Contents
ToggleEC- 601 Digital signal Processing
V Sem, EC
UNIT 1- Discrete-Time Signals And Systems
Q.1) Write about discrete time system with the help of examples.
(RGPV May 2024)
Q.2) Describe the classification of discrete time systems.
(RGPV May 2024)
Q.3) Explain in detail about different representations of discrete time signals.
(RGPV May 2023)
Q.4) State stability, causality and invertible properties of discrete time LTI system.
(RGPV May 2023)
Q.5) Define System. Determine whether the system
y[n] = 2x[n] * u[n] is
i) Memoryless
ii) Stable
iii) Time invariant
iv) Causal
(RGPV May 2022)
Q.6) Define the terms: linearity, time invariance and causality for a discrete time system.
(RGPV May 2022)
Q.7) Explain the classification of discrete time signals and systems.
(RGPV May 2022)
UNIT 2- The Z-Transform
Q.1) Determine the z-transform of an anticausal exponential sequence given as
x[n] = -αn μ[-n-1]
(RGPV May 2024)
Q.2) Describe the concept of region of convergence of a rational z-transform.
(RGPV May 2024)
Q.3) Determine the inverse z-transform via partial fraction expansion of the given function: 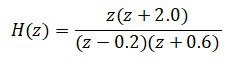
(RGPV May 2024)
Q.4) Write about the convolution property of z-transform.
(RGPV May 2024)
Q.5) Prove the following properties of Z.T.
i) Convolution in time
ii) Scaling in time domain
(RGPV May 2023)
Q.6) Determine the Inverse Z.T. of the 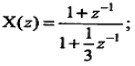
ROC: Re\{z\} > 1/3
(RGPV May 2023)
Q.7) Determine the Inverse Z.T. of the 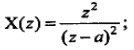
ROC: Re\{z\} > a
(RGPV May 2023)
Q.8) Find inverse z-transform of
![]()
(RGPV May 2023, 2022)
Q.9) Describe 2-transform and its properties.
(RGPV May 2022)
Q.10) Find the transfer function of the given signal flow graph of the system.
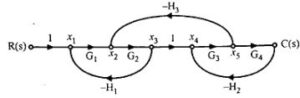
(RGPV May 2022)
UNIT 3- Frequency Analysis Of Discrete Time Signals
Q.1) What is concept discrete Fourier series? Drive an expression for it.
(RGPV May 2024)
Q.2) Illustrate the properties of discrete Fourier series.
(RGPV May 2024)
Q.3) Determine the 4-point circular convolution of the two length-4 sequences g[n] and h[n] given by g[n]={1 2 0 1 3, h [n] = { 2 2 1 1}, 0 <= n <= 3.
(RGPV May 2024)
Q.4) Derive the following properties of DFS.
i) Time shifting
ii) Time reversal
iii) Convolution
(RGPV May 2023)
Q.5) Explain DFS (Discrete Fourier Series) and its properties.
(RGPV May 2022)
Q.6) Find circular convolution for the following sequences x1(n) = {1, 2, 3, 4} and x2(n) = {1, 2, 1, 2} .
(RGPV May 2022)
UNIT 4- Efficient Computation of the DFT
Q.1) Define DFT and write about some important properties of it.
(RGPV May 2024)
Q.2) What is FFT? Derive an expression for it.
(RGPV May 2024)
Q.3) Given x[n] = {1, 2, 3, 4, 4, 3, 2, 1} find X(k) using DIF FFT algorithm.
(RGPV May 2024)
Q.4) Find the DFT of a sequence x(n) = (1/2)n u(n).
(RGPV May 2023)
Q.5) Determine the DFT of a sequence X(n) = {1, 1, 0, 0} .
(RGPV May 2023)
Q.6) Determine DFT of the sequence x(n) = {1,0,0,0} using FFT algorithm.
(RGPV May 2023)
Q.7) Determine the 4 – point IDFT of the sequence x[k] = {1, – j, 0, j} using DIT-FFT algorithm.
(RGPV May 2023)
Q.8) Compute 8-point DFT of the sequence
x(n) = {1, 1, 1, 1, 1, 1, 0, 0}
(RGPV May 2022)
Q.9) Compute the FFT for the sequence x(n) = n + 1 where N = 8 using the DIT algorithm.
(RGPV May 2022)
Q.10) Explain about decimation in frequency FFT algorithm.
(RGPV May 2022)
Q.11) Compute DFT of the sequence x(n)=( 1, 2, 3, 4, 4, 3, 2, 1 ) using the DIF FFT algorithm.
(RGPV May 2022)
UNIT 5- Digital Filters Design Techniques
Q.1) Determine the impulse response of the given sequence
y[n] = α1x[n]+ α2x[n-1]+α3x[n-2]+α4x[n-3]
(RGPV May 2024)
Q.2) Write about the design techniques for the FIR filters.
(RGPV May 2024)
Q.3) Convert the analog filter into digital filter whose system function is
![]()
Use the impulse invariant technique. Assume T=1s.
(RGPV May 2024)
Q.4) Outline the steps involved in the design of FIR filter using Hanning window.
(RGPV May 2023)
Q.5) Write the magnitude and phase functions of FIR filter when impulse response is symmetric and N is odd.
(RGPV May 2023)
Q.6) Explain briefly about different structures in FIR systems.
(RGPV May 2022)
Q.7) Discuss the characterization of IIR filters and compare with FIR filters.
(RGPV May 2022)
EXTRA QUESTIONS-
Q.1) Find the impulse response of the system described by the following difference equation: Assume all initial conditions are zero.
y(n) – 2y(n – 1) + 4y(n – 2) = x(n) + x(n – 1)
(RGPV May 2023)
Q.2) Write short notes on any two of the following:
i) Comparison of Butterworth and Chebyshev filter
ii) Properties of convolution sum
iii) R.O.C of Z-Transform
iv) Circular convolution
(RGPV May 2023)
Q.3) Write short notes on:
i) DFT
ii) Bilinear transformation method
iii) Rectangular window
iv) Block diagram
(RGPV May 2022)
— Best of Luck for Exam —

