Important RGPV Question

EX-405 (Control System)

IV Sem, EX

UNIT 1 Modelling of Dynamic Systems

Q.1 What is a mason gain formula? Explain each component of the formula and mention its advantages over block diagram reduction techniques.

(RGPV Nov 2023) 

Q.2 Obtain the overall transfer function C/R from the signal flow graph shown.

(RGPV Nov 2023) 

Q.3 Determine the transfer function for the block diagram shown in Figure.

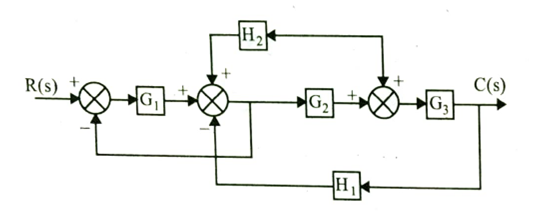
Distinguish between Open loop control system and closed loop control system.

(RGPV June 2023) 

Q.5 Find the transfer function using Mason’s gain equation.

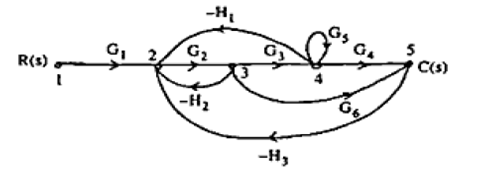
(RGPV June 2023) 

Q.6 Determine the transfer function X1(s)/F(s) for the system shown below.

(RGPV June 2023) 

Q.7 The block diagram of a unity feedback (negative) system is shown in figure. Determine the steady state error for unit ramp input when K-400. Also determine the value of K for which the steady state error to unit ramp will be 0.02.

(RGPV June 2023) 

Q.8 What are open and closed loop transfer system? What are the components of control systems?

(RGPV June 2020) 

Q.9 What is Mason’s gain formula? Simplify the given expression and find x5 / x1

(RGPV June 2020)

Q.10 Write short notes Tacho Generators

(RGPV June 2020) 

Q.11 State the advantages and disadvantages of closed loop system.

(RGPV May 2019) 

Q.12 Specify the time domain specification.

(RGPV May 2019) 

Q.13 State and explain the Mason’s gain formula.

(RGPV May 2019) 

Q.14 Derive the transfer function and develop the block diagram of armature control DC servo motor.

(RGPV May 2019) 

Q.15 Write short notes on (any two)

a) Servomotors

b) Potentiometer

c) Steeper motor

(RGPV May 2019) 

 

UNIT 2 Time-domain Analysis of closed loop Systems

Q.1 Explain time response of first order system to unit step and unit ramp input. Find the steady state error response for both.

(RGPV Nov 2023) 

Q.2 What are the standard test signals used in time domain analysis, explain each one in detail?

(RGPV Nov 2023) 

Q.3 Discuss the derivative and integral control in detail.

(RGPV Nov 2023) 

Q.4 Explain time response of first order system to unit step and unit ramp input. Find the steady state error response for both. 

(RGPV June 2023) 

Q.5 Discuss the proportional and integral control in detail.

(RGPV June 2023) 

Q.6 A unity feedback-system has an open loop transfer function G(s)H(s) Design a phase lag compensator to achieve the followings specifications. Velocity error constants Kv = 5. Phase margin= 45°.

(RGPV June 2022) 

Q.7 Derive the steady state error for type one system with unit step, ramp and parabolic inputs.

(RGPV June 2022) 

Q.8 Consider a type I unit feedback system with an OLTF is specified that Kv = 12 sec-1 and Φpm = 40°. Design lead compensator to meet the specifications.

(RGPV June 2022) 

Q.9 Obtain the steady state erroress of type-0 type-1 and type-2 systems for standard inputs.

(RGPV June 2022) 

Q.10 Distinguish between Open loop control system and closed loop control system.

(RGPV June 2022) 

Q.11 Name any two compensation techniques employed in the design of control systems.

(RGPV June 2022) 

Q.12 Derive the response of second order system with unit step response.

(RGPV June 2022) 

Q.13 What is Steady state error? Find the steady state error for a ramp input of a unity feedback control system with open loop transfer function

(RGPV June 2020) 

Q.14 Find Kp, Kv, Ka for a system with open loop transfer function as

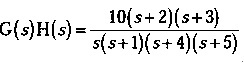
input is r(t)=3+t+t².

(RGPV June 2020) 

Q.15 A unity feed back system is characterized by an open loop transfer function G(s)=K/s(s+5). Determine the gain K so that the system will have a damping factor of 0.7. For this value of K determine the natural frequency of the system. It is subjected to a unity step input. Obtain the closed loop response of the system in time domain.

(RGPV May 2019) 

Q.16 Derive the expressions for frequency domain specifications of a second order system.

(RGPV May 2019) 

Q.17 Given the open loop transfer function of a unity feedback system G(s)=1/5(3+5)(1+2s). Draw the Bode plot and measure from the plot the frequency at which the magnitude is 0 dB.

(RGPV May 2019) 

Q.18 What are the standard test signals used in time domain analysis?

(RGPV May 2019)

 

UNIT 3 Stability 

Q.1 Comment on the stability of the system whose characteristic equation is given by s5+2s4+3s3+68²+25+10.

(RGPV Nov 2023) 

Q.2 Sketch the root locus for a system having transfer function

(RGPV Nov 2023) 

Q.3 Determine the RH stability of given characteristic equation, s4 + 8s3 + 18s²+16s + 5=0.

(RGPV June 2023) 

Q.4 Sketch the root locus for the unity feedback system whose open loop transfer function is

G(s)H(s) =  K/ [s (s+4) (s²+4s+20)]

(RGPV June 2023) 

Q.5 Using Routh-Hurwitz criterion determine the relation between K and T so that unity feedback control system whose open loop transfer function given below is stable.

(ii) Determine the modified relation between K and T if all the roots of characteristic equation as determined in (i) are to lie to the left of the line S = -1 in S-plane.

(RGPV June 2022) 

Q.6 What are the important features of open loop control system.

(RGPV June 2022) 

Q.7 Derive the expression for steady state error of the closed loop system in terms of generalized error coefficients.

(RGPV June 2022) 

Q.8 Define and derive the breakaway point on the root locus.

(RGPV June 2022) 

Q.9 Explain Routh-Hurwitz stability analysis.

(RGPV June 2020) 

Q.10 Discuss on stability of Root Locus.

(RGPV June 2020) 

Q.11 Give basics steps for construction of Root Locus.

(RGPV June 2020) 

Q.12 Explain the Routh’s criteria with an example. What are its limitations?

(RGPV May 2019) 

Q.13 Determine the stability of the closed loop system whose open loop transfer is 5(2s+1)/s(s+1)(1+3s) (1+0.5s), using Routh-Hurwitz criterion.

(RGPV May 2019) 

Q.14 What are the advantages of root locus?

(RGPV May 2019) 

Q.15 Explain the procedure to draw root locus of a given transfer function.

(RGPV May 2019) 

 

UNIT 4 Frequency 

Q.1 Consider the following polar plot shown in Figure below. If now a pole at origin and a pole at s-1/T2 are added, sketch the polar plot.

(RGPV Nov 2023) 

Q.2 Sketch the bode plot for the following transfer function and determine phase margin and gain margin.

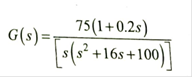
(RGPV Nov 2023) 

Q.3 Draw the polar plot for open loop transfer function for unity feedback system.

(RGPV Nov 2023) 

Q.4 State and explain Nyquist stability criteria.

(RGPV Nov 2023) 

Q.5 Consider the following polar plot shown in Figure below. If now a pole at origin and a pole at s=-1/T2 are added, sketch the polar plot.

(RGPV June 2023) 

Q.6 Describe the procedure for developing the polar plot

(RGPV June 2023) 

Q.7 Draw the Nyquist plot for the system whose open loop transfer function is

G(s)H(s) = K/[s(s+2) (s+10)] Determine the range of K for which the closed loop system is stable.

(RGPV June 2023) 

Q.8 Sketch the bode plot for the following transfer function and determine phase margin and gain margin.

G(s) = 75 (1+0.2s)/[s (s²+16s+100)]

(RGPV June 2023) 

Q.9 Define the following terms:

i) Settling time and relative stability

ii) phase margin and gain margin.

(RGPV June 2022) 

Q.10 Test the stability of the unity feedback system G when K=10 using Nyquist criterion and then find the range of K for stability.

(RGPV June 2022) 

Q.11 Explain in detail about Gain and Phase Margins.

(RGPV June 2020) 

Q.12 For a closed loop control system G(s)= 100 / s(s + 8), H(s) = 1. Determine the resonant peak and resonant frequency.

(RGPV June 2020) 

Q.13 Draw Polar plot of

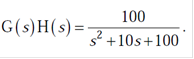
(RGPV June 2020) 

Q.14 Write short notes Nyquist stability analysis

(RGPV June 2020) 

Q.15 State and prove Nyquist stability theorem.

(RGPV May 2019)

 

UNIT 5 Design of Control System 

Q.1 What is lag-lead compensator? Under what conditions it is employed? Explain.

(RGPV Nov 2023) 

Q.2 Obtain the solution of state equation and list the properties of state transition matrix.

(RGPV Nov 2023) 

Q.3 Write a short notes on Eigen values and Eigen vectors

(RGPV Nov 2023) 

Q.4 Draw the electrical circuit diagram that represents the Lead-Lag compensator and explain in detail.

(RGPV June 2023) 

Q.5 Given the state equations below, write the transfer function for this system. Assume the output variable in the transfer function is y(t) which is equal to the state variable x1.

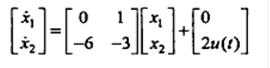
(RGPV June 2023) 

Q.6 Derive an expression for peak time tp of an underdamped second order systems subjected to step input.

(RGPV June 2022) 

Q.7 Write short notes on:

i) Need of compensator

ii) Asymptotes

(RGPV June 2022) 

Q.8 Derive the expression of transfer function of lead compensator. What are the effects of phase lead compensation?

(RGPV June 2022) 

Q.9 What is Lag-Lead compensator?

(RGPV June 2020) 

Q.10 Find the state transition matrix for

(RGPV June 2020) 

Q.11 What are Servomotors (AC and DC)?

(RGPV June 2020) 

Q.12 What are Proportional and Derivative controller.

(RGPV June 2020) 

Q.13 Write short notes PID controllers

(RGPV June 2020) 

Q.14 Discuss the effect of PD and PI on performance of a control system.

(RGPV May 2019) 

 

— Best of Luck for Exam —