Table of Contents
ToggleImportant RGPV Question
ME-404 (Fluid Mechanism)
IV Sem, ME
UNIT-1 INTRODUCTION
Q.1) With the help of a neat sketch describe the geometry of a single point cutting tool.
RGPV June 2013
Q.2) Define density, specific volume, weight density and specific gravity of fluid.
RGPV June 2014
Q.3) Write short notes on – Vapour pressure and cavitation.
RGPV June 2017
Q.4) Define compressibility. How it is related to bulk modulus of elasticity?
RGPV Dec 2016
Q.5) Explain bulk modulus of elasticity.
RGPV Dec 2014
Q.6) 5.2 litres petrol weighs 14 N. Calculate the specific weight, mass density, specific volume and specific gravity of petrol with respect to water.
RGPV June 2014
Q.7) A cylinder contains 0.75 m³ of gas at 20°C and 2.5 bar pressure. After compression, the volume gets reduced to 0.15 m³. Determine final pressure and bulk modulus of compressed air if compression takes place under- (i) Isothermal conditions (ii) Adiabatic conditions (γ =1.4).
RGPV June 2013
Q.8) State and explain the Newton’s law of viscosity.
RGPV June 2015
Or
Define the Newton’s law of viscosity.
RGPV June 2016
Q.9) What is meant by viscosity of a liquid? How does it manifest and in what units is it measured?
RGPV June 2012
Q.10) What is Newton’s law of viscosity? What is the effect of pressure and temperature on viscosity?
RGPV Dec 2014 2017
Q.11) Define and distinguish between the following set of fluid properties- (i) Specific weight and mass density (ii) Dynamic viscosity and kinematic viscosity.
RGPV June 2013
Q.12) Draw the stress-strain relationship for different types of fluid. Also give examples.
RGPV June 2011
Q.13) Determine the resistance offered to the downward sliding of a shaft of 400 mm diameter and 0.1 m length by the oil film between the shaft and a bearing of ID 402 mm. The kinematic viscosity is 2.4 x 104 m/s and density is 900 kg/m³. The shaft is to move centrally and axially at a constant velocity of 0.1 m/s.
RGPV June 2014
Q.14) Explain various pressure measurement terms.
RGPV Dec 2014
Or
Define atmospheric, gauge, vacuum and absolute pressure.
RGPV June 2015
Q.15) State the Pascal’s law and its application.
RGPV June 2016
Or
State Pascal’s law.
RGPV Dec 2015
Or
State and prove Pascal’s law of fluid pressure.
RGPV Dec 2017
Q.16) Define the following- (i) Centre of buoyancy (ii) Metacentre (iii) Centre of pressure.
RGPV Dec 2013, June 2017
Q.17) What do you mean by centre of pressure? Explain.
RGPV May 2019
Or
What is meant by centre of pressure? How does it vary with depth of fluid ?
RGPV Dec 2015
Q.18)Derive an expression for the total pressure force and centre of pressure for a vertical plane surface submerged in a liquid.
RGPV Dec 2006, 2012, 2017
Q.19) Show that if ‘B’ is the centre of buoyancy and ‘M’ is the metacentre of a partially immersed floating body then BM=I/V where I is the second moment of area of the surface of floatation about the longitudinal axis and ‘V’ is the immersed volume.
RGPV Dec 2016
Q.20) Discuss the conditions of equilibrium of a floating body.
RGPV Dec 2015
Or
Write short note on- Different conditions of equilibrium.
RGPV June 2017
Q.21) 4 m x 4m square tank is filled with water. Height of tank is 2 m. Find total pressure and pressure centre on vertical wall.
RGPV May 2019
Q.22) A rectangular plane surface is 2 m wide and 3 m deep. It lies in vertical plane in water. Determine the total pressure and position of centre of pressure on the plane surface when its upper edge is horizontal and– (i) Coincides with water surface
(ii) 2.5 m below the free water surface.
RGPV June 2017
Q.23) Find the volume of the water displaced and position of centre of buoyancy for a wooden block of width 2.5 m and depth 1.5 m, when it floats horizontally in water. The density of wooden block is 650 kg/m³ and its length 6.0 m.
RGPV May 2018
Q.24) A channel of trapezoidal section of 1.5 m at bottom and 3.0 m at the top with equal side slopes is provided with a vertical gate. The depth of water when the channel is running full is 1.2 m (the top of the gate at water level). Determine the total pressure and the centre of pressure.
RGPV Dec 2014
Q.25) A wooden cylinder of specific gravity of 0.6 and circular in cross-section is required to float in oil of specific gravity of 0.90. Find the length/diameter (L/D) ratio for cylinder to float with its longitudinal axis vertical in oil.
RGPV June 2016
Or
A wooden cylinder of specific gravity 0.6 and circular in cross-section is required to float in oil (Specific gravity 0.90). Find L/D ratio for the cylinder to float with its longitudinal axis vertical in oil, where L is height of cylinder and D is its diameter.
RGPV Dec 2015
Q.26) A wooden log of 0.6 m diameter and 5 m length is floating in river water. Find the depth of the wooden log in water when the specific gravity of the log is 0.8.
RGPV Dec 2011
UNIT-2 FLUID KINEMATICS
Q.1) Explain the methods of describing fluid motion.
RGPV Dec 2014
Q.2) Differentiate between the Eulerian and Lagrangian method of representing fluid motion.
RGPV June 2013
Q.3) What are the different types of flow? Differentiate compressible and incompressible flow.
RGPV May 2019
Q.4) Distinguish between uniform flow and non-uniform flow.
RGPV June 2016
Q.5) Describe one-dimensional, two-dimensional and three-dimension flows with examples and neat sketches.
RGPV Dec 2011
Q.6) Define and distinguish between
(i) Rotational and irrotational flow
(ii) Uniform and non-uniform flow
(iii) Steady and unsteady flow.
RGPV Dec 2016
Q.7) Write short notes on- (i) Path line (ii) Specific weight (iii) Steady flow (iv) Laminar flow (v) Streak line (vii) Uniform flow. (vi) Rotational flow
RGPV May 2019
Q.8) Write about –
(i) Path lines
(ii) Streak lines
(iii) Streamlines and stream tube.
RGPV May 2018
Q.9) The velocity distribution for a three-dimensional flow is given by- V = axi+ayj-2azk Find the equation of streamline passing through the position vector r=2i+2j+4k.
RGPV June 2013
Q.10) Derive an expression for continuity equation for three-dimensional flow.
RGPV Nov 2018
Or
Derive the continuity equation for three-dimensional flow.
RGPV May 2018
Or
Derive an expression for continuity for a three-dimensional steady incompressible flow.
RGPV Dec 2012, 2017
Or
Derive continuity equation for 3-dimensional incompressible flow.
RGPV Dec 2014
Or
Derive the continuity equation in cartesian co-ordinates.
RGPV June 2015
Or
Write short note on-General three-dimensional equation of continuity.
RGPV June 2017
Q.11) The velocity components in a two-dimensional flow are

Show that these velocity components represent a possible case of an irrotational flow.
RGPV Dec 2015
Q.11) Determine the convective acceleration in the middle of the pipe which converges uniformly from 60 cm to 30 cm diameter over a length of 3 m. The rate of flow is 0.04 m/s. If the rate of flow changes from 0.04 m/s to 0.08 m³/s in 40 seconds, determine the total acceleration in the middle of the pipe at the 20th second.
RGPV Dec 2014
Q.12) Explain uniform flow with source and sink.
RGPV Dec 2015
Q.13) Define – Circulation, vorticity, convective and local acceleration.
RGPV Dec 2013
Q.14) Explain about velocity potential and stream function.
RGPV May 2018
Or
Derive an expression for-
(i) Stream function
(ii) Velocity function.
RGPV Dec 2011
Or
Define and explain velocity potential and stream function.
RGPV June 2015
Or
Define velocity potential function and stream function.
RGPV Dec 2015
Or
Define the term velocity potential function and stream function.
RGPV June 2016
Q.15) Prove that the stream function and potential function lead to orthogonality of streamlines and equipotential flow lines.
RGPV June 2014, Dec. 2017
Q.16)Explain the following in detail – (i) Circulation (iii) Sinks (ii) Sources (iv) Flow net.
RGPV Nov 2018
Q.17) If the velocity field is given by u=16y-8x, v=8y-7x, find the circulation around the closed curve defined by x=4, y=2,x=8, y=8.
RGPV Dec 2013
Q.18) Given that u = x²-y2 and v= -2xy, determine the stream function and potential function for the flow.
RGPV June 2014
Q.19) The velocity components in a two-dimensional flow field for an incompressible fluid are as follows-
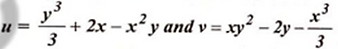
Obtain an expression for stream function
RGPV June 2017
Q.20) Define the source flow. Derive the equation of stream function Also plot the streamlines.
RGPV June 2016
UNIT-3 FLUID DYNAMICS
Q.1) State Bernoulli’s theorem. Mention the assumptions made.
RGPV May 2018
Or
State Bernoulli’s theorem. What are the assumptions made in Bernoulli’s equation?
RGPV Dec 2017
Q.2) State the Bernoulli’s equation of fluid flow.
RGPV June 2016
Q.3) What is Euler’s equation of motion? Derive Bernoulli’s equation from Euler’s equation. Discuss the assumptions made.
RGPV June 2014
Q.4) Derive Bernoulli’s theorem for steady flow of an incompressible fluid from consideration of momentum.
RGPV Dec 2015
Or
Derive Bernoulli’s equation for frictionless flow. Apply the necessary corrections for frictional flow.
RGPV Nov 2018
Q.5) What are the limitations of the Bernoulli’s equation?
RGPV June 2015
Q.6) What is Bernoulli’s theorem? What are the limitations of Bernoulli’s theorem?
RGPV May 2019
Or
State Bernoulli’s theorem and give its limitations.
RGPV Dec 2014
Q.7) Discuss some applications of Bernoulli’s equation.
RGPV June 2014
Q.8) What is venturimeter ? State the expression of discharge through venturimeter.
RGPV Dec 2015
Q.9) Sketch a venturimeter and manometer arrangement, apply the steady flow energy equation and derive an expression for actual flow rate.
RGPV Dec 2016
Or
Discuss the working principle of venturimeter and derive the equation Or for actual discharge through it.
RGPV June 2016
Q.10) What is venturimeter? Derive an expression for discharge through venturimeter.
RGPV May 2019
Q.11) What is impulse momentum equation? Give its engineering applications.
RGPV Dec 2014
Q.12) Define and explain the significance of the kinetic energy correction factor and the momentum correction factor. Suggest their practical values for laminar and turbulent flows.
RGPV June 2011, 2012
Or
Explain kinetic energy correction factor and momentum correction factor.
RGPV Dec 2014
Q.13) State the moment of momentum equation and its application.
RGPV June 2016
Or
Define moment of momentum equation. Where this equation is used?
RGPV Dec 2015
Or
What is the moment of momentum equation?
RGPV June 2015
Or
Write short note on – The moment of momentum equation.
RGPV Dec 2017
Q.14) An orifice meter with orifice diameter 10 cm is inserted in a pipe of 20 cm diameter. The pressure gauges fitted upstream and downstream of the orifice meter gives readings of 19.62 N/cm² and 9.81 N/cm² respectively. Coefficient of discharge is given as 0.6. Find the discharge of water through pipe.
RGPV Dec 2015
Q.15) A liquid with specific gravity 0.8 flows at the rate of 3 Us through a venturimeter of diameters 6 cm and 4 cm. If the manometer fluid is mercury, determine the value of manometer reading x.
RGPV June 2014
Q.16) A venturimeter of 200 mm x 100 mm is installed in a vertical pipe carrying oil of specific gravity 0.80. The throat is 0.5 m above the entrance. A differential mercury manometer shows a deflection of 400 mm. Calculate the oil flow rate and also the pressure difference beween the entrance and throat. Assume C=0.98.
RGPV Dec 2014
Q.17) A horizontal venturimeter with inlet and throat diameters 240 mm and 120 mm respectively is used to measure the flow of water. The pressure intensity at inlet is 130 kN/m² (gauge), while the vacuum pressure head at the throat is 150 mm of mercury. Assuming that 3% of pressure head is lost in between inlet and throat, find the coefficient of discharge and rate of flow.
RGPV Nov 2018
Q.18) A 45° reducing pipe bend in a horizontal plane has an inlet diameter of 300 mm and outlet diameter of 150 mm. The pressure at the outlet is 20 kPa gauge and rate of flow of water through the bend is 0.09 m³/s. Neglecting friction, determine the magnitude and direction of the force required to keep the bend in position. Neglect the weight of the water in the bend.
RGPV Nov 2018
Q.19) Water enters a reducing pipe horizontally and comes out vertically in the downward direction. If the inlet velocity in 5 m/sec and pressure is 80 kPa gauge and the diameters at the entrance and exit sections are 30 cm and 20 cm respectively, calculate the components of reaction acting on the pipe.
RGPV Dec 2016
Q.20) What is Magnus effect? Explain.
RGPV June 2014
UNIT-4 FLOW THROUGH PIPES
Q.1) Describe Reynold’s experiment to demonstrate the two types of flow.
RGPV June 2014
Or
Explain the Reynold’s apparatus with the help of neat sketch.
RGPV Dec 2013
Or
Explain Reynold’s experiment.
RGPV Dec 2014
Q.2) Explain about Reynold’s experiment and significance of Reynold number.
RGPV May 2018
Or
Describe Reynold’s experiment to demonstrate the laminar and turbulent fluid flows. How is the type of flow related to Reynold’s number?
RGPV June 2012
Or
Write short note on – Reynold’s experiment of Reynold’s number.
RGPV Dec 2012
Or
What is Reynold’s number? Give its significance.
RGPV Dec 2014
Q.3)What do you understand by laminar flow? What factor decides the type of flow in pipes?
RGPV May 2018
Q.4)Differentiate/Distinguish between laminar and turbulent flow.
RGPV Dec 2014, 2015, June 2016
Q.5) State the shear stress and its distribution over a fluid flow through circular pipe.
RGPV June 2016
Q.6) Derive an expression for Hagen-Poiseuille equation and statt the assumptions made.
RGPV Dec 2013
Or
Derive the Hagen-Poiseuille’s equation and state the assumptions made.
RGPV Dec 2010, June 2011, Dec 2016
Or
Derive Hagen-Poiseuille equation.
RGPV Dec 2014
Or
Derive the Hagen-Poiseuille formula.
RGPV June 2016
Q.7) Obtain an expression for velocity distribution in terms of average velocity for smooth pipes.
RGPV May 2018
Q.8) Write a note on losses during flow through a pipe.
RGPV Dec 2015
Q.9)A fluid of density 1200 kg/m³ and viscosity 0.5 poise is flowing at a rate of 5 m³/min in a circular pipe of cross-section of 1 m². Is the flow laminar or turbulent? Can you predict the maximum velocity of the fluid in the pipe?
RGPV June 2015
Q.10) A pipe 100 mm in diameter and 40 m long conveys water at: velocity of 2.5 m/s. If a 200 mm diameter pipe replaces central 20 m length of pipe. Find the saving in head loss. Assume that changes in section are sudden. Take f= 0.01 and coefficient of contraction C-0.62.
RGPV Dec 2015
Q.11) A crude oil of viscosity 0.9 poise and relative density 0.9 is flowing through a horizontal circular pipe of diameter 120 mm and length 12 m. Calculate the difference of pressure at the two ends of the pipe. If 785 of the oil is collected in a tank in 25 seconds.
RGPV June 2015
Q.12) The friction factor in a laminar flow through pipe is 0.016. What is its Reynold number?
RGPV Dec 2015
Q.13) Find power loss due to friction in a circular pipe when length of pipe 300 m, diameter 15 cm and discharge 28 Us and f=0.01.
RGPV May 2019
Q.14) A valve is attached to hand pump of 1200 m length. Water is flowing with 4 m/s. If 25 s elapsed to close the valve, find the pressure intensity due to water hammer.
RGPV May 2019
Q.15) A pipe 10 cm in dia. and 1000 m long is used to pump oil of viscosity 3.5 poise and specific gravity 0.92 at the rate of 1200 lit/min. The first 300 m of the pipe is laid along the ground sloping upwards at 10° to the horizontal and the remaining pipe is laid on the ground sloping upwards at 15° to the horizontal. State whether the flow is laminar or turbulent. Determine the pressure required to be developed by the pump and the power of the driving motor if the pump efficiency is 60 percent. Assume suitable data for friction coefficient, if required.
RGPV June 2013
Q.16) An oil of specific gravity 0.82 and kinematic viscosity 16 x 10-6 m²/s flows in a smooth pipe of 8 cm diameter at a rate of 2 l/s. Determine whether the flow is laminar or turbulent. Also calculate the velocity at the centre line and the velocity at a radius of 2.5 cm. What is head loss for a length of 10 m? What will be the entry length? Also determine the wall shear.
RGPV June 2014
UNIT-5 INTRODUCTION TO BOUNDARY LAYER THEORY
Q.1) Describe the laminar and turbulent boundary layer flow over a flat plate.
RGPV Dec 2011
Q.2) State the assumptions under which the boundary layer equations for flow over a flat plate are valid. Explain with a neat sketch the boundary layer characteristics when a liquid is flowing over a flat plate.
RGPV Nov 2018
Q.3) Derive the Von Karman momentum integral equation.
RGPV June 2017
Q.4) What do you mean by separation of boundary layer? What is the effect of pressure gradient on boundary layer separation?
RGPV Dec 2017
Or
Write short note on separation of fluid flow.
RGPV June 2014
Q.5) What characterises the stagnation point?
RGPV June 2013
— Best of Luck for Exam —
